Modelling photos with graphs

Adrian Oldknow has developed some activities that involve modelling photographs with graphs. A photo can be copied from a webpage and pasted into software that allows a graph to be superimposed. Recent versions of Autograph, Derive, Geometer's Sketchpad and Cabri Geometry are suitable for this. Three sections of the Problem Pictures Themes resource have photographs that can be used in this way. This modelling activity offers a learning environment which encourages experimentation.

Sail sculpture

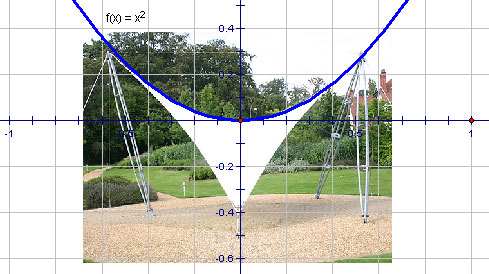
With the software used here, the two red dots are 'handles' which can be used to move the axes around. With some care, it was possible to superimpose the graph of x² on top of the U-shaped curve. The curve in this photograph is a close match to a parabola.

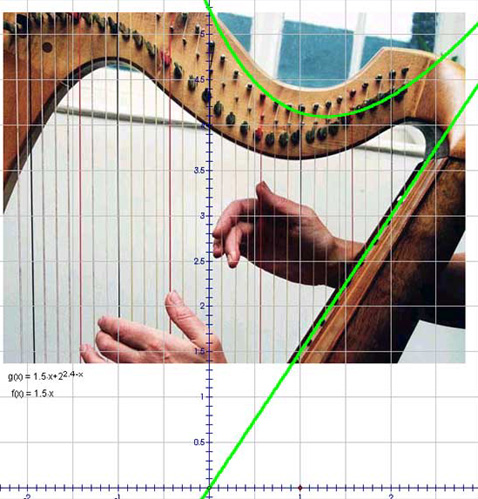
The shape of a harp

Why are harps such an unusual shape? Is it decorative or functional?

On this harp the red strings and black strings mark out the octaves. Physics tells us that doubling the length of a string should lower the pitch by one octave. But this is only true if the strings are made of the same material and are under the same tension. Let us assume this as an approximation.

I used square axes with one unit equal to one octave. I drew a straight line along the baseboard which passed through the origin.

I wanted to plot a function that describes the top of the strings. This must equal the length of the string (2^{a - x} where a is a constant) plus the height of the baseboard (the straight line already plotted).

The result shows a curve which is only a crude approximation to the shape of the harp. In practice harps use strings made from different weights of material and under different tensions.

For further information see the articles referenced on Adrian Oldknow's website.